ASCENDANCE (météorologie)

ASCENDANCE (météorologie)

Dans le langage aéronautique, et spécialement dans la littérature ayant trait au vol à voile, on donne le nom d’ascendance à un courant aérien dirigé vers le haut et susceptible d’imprimer un mouvement ascendant à un avion ou à un planeur qui traverse ce courant.

Peu à peu, dans le vocabulaire météorologique, on tend à donner le nom d’ascendance à tout mouvement vertical de l’air dirigé vers le haut, quelle que soit son échelle de grandeur ou son intensité.

Par opposition, un courant aérien dirigé vers le bas est appelé descendance, ou rabattant , ce dernier terme s’appliquant surtout aux descendances imprimées par le relief. Un mouvement général d’affaissement de l’air, tel qu’il s’en produit dans les anticyclones par suite de la divergence des vents dans les basses couches de l’atmosphère, porte le nom de subsidence .

Les phénomènes d’ascendance peuvent exister dans l’atmosphère à des échelles fort différentes. De petits tourbillons aériens (turbulence) dont le diamètre est de l’ordre du décimètre ou du mètre, et dont l’axe est plus ou moins voisin de l’horizontale, comportent une partie ascendante (ascendance) et une partie descendante. Le passage successif, en un lieu, de tels tourbillons emportés par les courants aériens généraux, détermine les fluctuations de la vitesse du vent qui constituent les rafales . La vitesse verticale de l’air dans de tels tourbillons peut atteindre l’ordre de grandeur du mètre par seconde.

À l’autre extrémité de l’échelle figurent les grands mouvements d’ascendance synoptique de masses d’air chaud sur des masses d’air froid plus denses, le long de surfaces de discontinuité atmosphériques appelées fronts . De telles ascendances frontales peuvent se produire sur des étendues dont la superficie est de l’ordre de celle de la France. La composante verticale moyenne de la vitesse de l’air dans de tels mouvements ne dépasse pas l’ordre de grandeur de quelques centimètres ou du décimètre par seconde.

Entre ces deux extrêmes prennent place les phénomènes d’ascendance dus à la convection . Le processus de convection, qui sera étudié par la suite, prend naissance lorsque la surface du globe devient nettement plus chaude que l’air qui est à son contact. Cette particularité se produit soit sous l’effet de l’échauffement du sol par absorption de l’énergie du rayonnement solaire, soit par suite de l’irruption d’une masse d’air froid sur un sol relativement chaud. La convection se traduit par l’ascendance de «bulles» d’air dont le déplacement est nécessairement compensé par des mouvements descendants de l’air environnant. C’est le phénomène de convection qui donne naissance aux nuages du genre cumulus ou cumulo-nimbus qui portent de ce fait le nom de nuages convectifs. Les vitesses verticales correspondantes sont fréquemment de l’ordre de plusieurs mètres par seconde et peuvent atteindre quelques décamètres par seconde (dans les cumulo-nimbus). Les dimensions horizontales de ces ascendances sont normalement de plusieurs décamètres et peuvent atteindre quelques hectomètres, dépendant en particulier de l’hétérogénéité du sol sous-jacent.

Enfin, mentionnons les ascendances de relief (ou ascendances dynamiques). Ces dernières, qui sont de l’ordre de quelques décimètres à quelques mètres par seconde, sont produites par l’ascension de l’air qui s’élève «au vent» d’une chaîne de montagnes ou de collines allongées perpendiculairement à la direction du vent pour redescendre ensuite «sous le vent» du relief (rabattant). Dans certaines conditions se développent également jusqu’à des altitudes élevées (parfois de 10 à 12 km lorsqu’il s’agit de chaînes importantes telles les Alpes ou les Pyrénées) des systèmes d’ondes de relief qui, en raison de leur permanence, de leur matérialisation fréquente par un nuage en bande (altocumulus) et des vitesses ascendantes de l’ordre de 5 à 10 mètres par seconde qu’on y rencontre, ont permis la réalisation d’impressionnants records d’altitude en planeur.

Turbulence

Il faut tout d’abord faire la distinction entre la turbulence considérée d’un point de vue météorologique dans un domaine déterminé (point de vue eulérien) et la turbulence que peut rencontrer un avion en vol (point de vue lagrangien).

Turbulence météorologique

Comme on l’a indiqué, la turbulence météorologique est due à l’existence de petits tourbillons de dimensions diverses dont les mouvements désordonnés apparaissent, à une échelle très considérablement supérieure, comme l’équivalent du mouvement d’agitation moléculaire dans un fluide au repos.

Il est impossible de songer à décrire ou étudier le comportement individuel de chacun de ces tourbillons, et seules certaines de leurs propriétés statistiques peuvent être atteintes.

Si l’on imagine que les plus grands tourbillons atmosphériques comportent en leur sein des tourbillons plus petits qui, à leur tour, enferment des tourbillons encore plus petits, il est évident que les petits tourbillons ont en moyenne pour effet de tendre à freiner ou à désorganiser les plus grands et qu’ils ont ainsi tendance à absorber une partie de leur énergie. Il y a donc un transfert d’énergie des grands tourbillons vers les petits et destruction finale de ces derniers par les forces de viscosité.

La turbulence peut naître d’une hétérogénéité de l’écoulement moyen de l’air, par exemple d’un fort gradient vertical du vent dû au frottement exercé par l’écoulement de l’air au contact de la surface du sol, ou encore par une discontinuité de la vitesse ou de la direction du vent selon la verticale. L’écoulement de l’air est en moyenne plus turbulent au-dessus de la terre qu’au-dessus de la mer. La turbulence peut aussi résulter, comme la convection – et en réalité on doit alors la considérer comme une forme de convection inorganisée –, de la formation de tourbillons, nécessaire pour assurer la diffusion de la quantité de chaleur disponible à la surface du globe.

Turbulence aéronautique

La turbulence aéronautique est celle dont les effets se traduisent sur un avion en vol par des secousses brutales ou de brèves accélérations verticales et horizontales. C’est un phénomène complexe puisqu’il fait intervenir les conditions de vol et les caractéristiques aérodynamiques de l’avion lui-même. Tel avion qui traverse une zone turbulente sera plus durement secoué qu’un autre, ou inversement. Mais il y a plus: un avion qui traverse une série d’ascendances et de descendances non liées à l’existence d’une turbulence sera soumis, à des intervalles très rapprochés, à des mouvements verticaux dirigés tantôt vers le haut, tantôt vers le bas, et éprouvera tous les effets d’une turbulence. C’est le cas notamment de la traversée par un avion rapide d’un système d’ondes tel qu’il s’en développe sous le vent du relief (ondes de relief ) et que tous les pilotes de vol à voile s’accordent à déclarer comme pratiquement dépourvus de toute turbulence.

La mise en service d’avions à réaction volant plus vite et à plus haute altitude que les avions à hélice a attiré l’attention sur un phénomène appelé turbulence en atmosphère claire (clear air turbulence , abrév. C.A.T.). Alors que le pilote d’un avion est prévenu, par l’observation visuelle de la présence d’un nuage convectif (éventuellement, de nuit, en détectant ce nuage grâce à son radar de bord), qu’il risque de pénétrer dans une zone de turbulence aéronautique, et qu’il peut en conséquence chercher à éviter cette zone ou, pour le moins, réduire la vitesse de l’avion qui subira ainsi des accélérations moins fortes, ce même pilote se trouve désarmé lorsqu’il pénètre sans aucun signe précurseur dans une zone de turbulence en atmosphère claire.

On ne connaît pas encore la nature exacte de cette turbulence et on ne sait pas bien la localiser a priori. Mais il semble que, comme on l’a déjà signalé, la traversée par un avion rapide d’un système d’ondes de relief, non matérialisé, comme c’est souvent le cas, par des altocumulus lenticulaires ou en bandes, puisse engendrer une telle turbulence aéronautique.

D’autre part, on sait qu’il existe sous la tropopause et au voisinage des grands fronts atmosphériques des courants de vents très forts (dépassant parfois 300 km/h) appelés «courants-jets» (jet-streams ). Sur la bordure de ces courants, qui peuvent s’étendre au long de milliers de kilomètres sur quelques centaines de kilomètres de largeur et sur quelques kilomètres d’épaisseur, règne un fort gradient vertical et horizontal de vent; des tourbillons peuvent donc y prendre naissance. En réalité, on a fréquemment observé de la turbulence en atmosphère claire au voisinage des courants-jets et en particulier sur leur bordure froide (tournée vers le pôle), où l’analyse des conditions météorologiques faite à partir de sondages aérologiques montre que le gradient du vent est en général maximal.

Convection

Si l’on suppose un fluide enfermé entre deux parois métalliques horizontales (fig. 1) et que l’on chauffe très progressivement la paroi inférieure, le fluide au contact s’échauffe et l’agitation des molécules du fluide, qui est fonction de la température, se transmet de proche en proche à travers la totalité du fluide jusqu’à atteindre la paroi supérieure. Il y a donc eu transfert de chaleur, par conductibilité moléculaire, de la paroi inférieure à la paroi supérieure. Mais, si nous chauffons plus intensément, il arrivera un moment où la seule agitation moléculaire deviendra incapable d’assurer un transfert de chaleur suffisant et la température de la plaque inférieure s’élèvera, provoquant l’établissement d’un gradient vertical de température important.

Convection cellulaire

Cependant, l’échauffement demeurant modéré, on assiste à la formation d’une circulation cellulaire sous forme de tourbillons alternés (tourbillons de Bénard) dont la section affecte une forme hexagonale (en nid d’abeilles) ou carrée. D’après certains auteurs, la forme hexagonale prendrait place pour des gradients de température un peu plus faibles que pour la forme carrée qui, seule, serait stable (fig. 2). Dans la nature, un tel type de convection ne se produirait qu’en altitude (forme en dallage de certains altocumulus ou strato-cumulus) mais ne pourrait se produire au voisinage du sol en raison des irrégularités de celui-ci, ni même sur mer ou sur les étendues homogènes désertiques par suite du gradient vertical du vent et de la turbulence.

Convection en bulles ou en colonnes

En réalité, d’après les observations des pilotes de planeurs et d’après les mesures effectuées en vol par les météorologistes, les mouvements convectifs naturels s’opéreraient par «bouffées» d’air chaud ascendant qui pourraient, si l’échauffement du sol est suffisant, se transformer en une émission continue d’air chaud sous forme d’une colonne d’air ascendant.

Dans le premier cas (fig. 3), l’air, qui s’est échauffé au contact d’un sol plus chaud que l’environnement, se détache sous forme d’une «bulle» et est remplacé par de l’air plus frais venant latéralement combler l’espace libéré. La bulle se trouve ainsi coupée de sa base et il faut attendre un certain temps pour que l’air frais de remplacement s’échauffe et se détache à son tour sous forme d’une autre bulle. On conçoit que, si l’échauffement de l’air frais de remplacement est suffisamment rapide, un courant ascendant continu puisse se développer.

Ce type d’ascendances en bulles ou en colonnes porte le nom d’ascendances thermiques ou simplement thermiques . L’une des techniques du vol à voile (vol à voile thermique) consiste à maintenir le planeur le plus longtemps possible dans une telle bulle ou colonne en lui faisant décrire des orbes ou spirales de façon à gagner le plus d’altitude possible.

Décroissance de température

Décroissance de température adiabatique sèche

Qu’advient-il d’une telle bulle d’air chaud ascendant? Tout d’abord, puisque la pression atmosphérique diminue avec l’altitude, la bulle se dilate. Mais la dilatation d’un gaz s’accompagne d’un refroidissement (expérience du pneu de voiture que l’on dégonfle) de même que la compression s’accompagne d’un échauffement. On considère en général que, dans le cas de notre bulle ascendante, ce refroidissement est suffisamment rapide pour que les échanges de chaleur avec l’air environnant soient négligeables. Cette hypothèse a d’autant plus de chances d’être valable que la bulle est plus grosse; en effet, les échanges de chaleur s’effectuent à travers la «surface» qui sépare la bulle du milieu ambiant et cette surface croît comme le carré des dimensions de la bulle alors que la masse de la bulle est proportionnelle au cube (volume) de ses dimensions. Dans ces conditions, plus la bulle est volumineuse et plus la fraction de chaleur échangée avec le milieu ambiant devient petite par rapport à la quantité totale de chaleur transportée par la bulle.

En fait, l’expérience justifie très correctement la validité de cette hypothèse dont l’intérêt réside dans le fait que le processus d’évolution, étant alors un processus adiabatique , obéit à des lois thermodynamiques simples. En particulier, dans un tel processus, la température est liée à la pression par la loi:

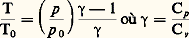est le rapport de la capacité thermique de l’air à pression constante (C^p ) et à volume constant (C^v ).

D’après cette loi, il est aisé de calculer que la température de la bulle ascendante diminue de 1 ⁰C chaque fois que la bulle s’élève de 100 mètres; c’est cette quantité que l’on nomme gradient adiabatique sec .

Décroissance de température adiabatique saturée

Mais cette décroissance de température selon la loi adiabatique sèche ne se poursuit pas indéfiniment, car il arrive un moment où la vapeur d’eau – toujours présente dans l’air atmosphérique – devient saturante. À partir de ce moment, toute élévation consécutive de la bulle se traduira par la condensation d’une partie de la vapeur d’eau sous forme de fines gouttelettes qui se déposent sur de microscopiques impuretés de l’air appelées noyaux de condensation. Mais la condensation de la vapeur d’eau s’accompagne de la libération d’une certaine quantité de chaleur (on peut aussi dire que, pour condenser de la vapeur d’eau, il faut lui retirer de la chaleur); c’est le phénomène inverse de l’évaporation, pour laquelle il y a lieu de fournir de la chaleur.

La libération de la chaleur latente de condensation a pour effet de diminuer la décroissance de température de notre bulle ascendante à partir du moment où elle atteint son niveau de condensation.

Le gradient adiabatique saturé a donc une valeur plus faible que le gradient adiabatique sec; il n’est pas indépendant de la température et de la pression et il est par conséquent impossible de lui assigner une valeur unique. Pour une température située aux environs de 10 ⁰C et pour une altitude de 1 à 2 kilomètres, sa valeur est voisine de 0,6 ⁰C par 100 mètres.

Diagrammes thermodynamiques

Dans la pratique courante, les problèmes relatifs à la température d’une bulle ascendante ou descendante, le calcul du niveau de condensation, du sommet des nuages correspondants, etc. se traitent graphiquement sur un diagramme thermodynamique. Un grand nombre de services météorologiques utilisent un diagramme (émagramme) comportant en abscisse une échelle linéaire de températures et en ordonnée une échelle logarithmique de pressions. Pour une meilleure utilisation du diagramme de la figure 4, l’axe des ordonnées souvent n’est pas perpendiculaire à l’axe des abscisses mais est fréquemment incliné à 45 degrés sur cet axe (système de coordonnées obliques).

Stabilité. Instabilité

La bulle ascendante, dont la température décroît constamment à mesure qu’elle s’élève, deviendra, à partir d’un certain niveau, plus froide que l’air environnant. À ce moment, la poussée d’Archimède, jusqu’alors dirigée vers le haut, se trouvera dirigée vers le bas et l’ascension de la particule consommera de l’énergie: elle sera freinée puis s’arrêtera. Plus froide, donc plus dense que l’air ambiant, elle aura tendance à redescendre.

On dit qu’une masse d’air est en équilibre stable, ou simplement stable, lorsqu’une particule d’air (bulle) déplacée verticalement à une petite distance de son niveau initial, sous l’effet d’une action perturbatrice très petite, tend à revenir à son niveau initial.

Si cette particule tend spontanément à s’éloigner de son niveau initial sous l’effet de l’action perturbatrice primitive, la masse d’air est dite instable. Si cette particule ne manifeste aucune tendance à quitter sa nouvelle position, la masse d’air est dite en équilibre indifférent.

Équilibre vertical d’une particule d’air

Pour étudier l’équilibre vertical d’une particule d’air, il est nécessaire de déterminer les forces qui s’exercent sur elle. Ces forces sont de deux sortes: forces de pesanteur qui s’exercent sur chacune des molécules qui constituent la bulle ou particule; forces de pression exercées par le milieu extérieur sur la surface idéale qui limite la particule.

On sait que les forces de pesanteur se réduisent à une résultante unique qui est le poids P de la particule, vertical et dirigé vers le bas et appliqué au centre de gravité de la particule. Les forces de pression se réduisent également à une résultante unique R, verticale et dirigée vers le haut, qui est la poussée d’Archimède. Si T et T sont les températures respectives de l’air de la bulle et de l’air environnant et si p et p sont les pressions initiales et finales de la bulle dans son déplacement vertical, les lois des gaz permettent de calculer le travail mis en jeu pendant ce déplacement:

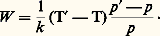Cette formule montre que le travail W est proportionnel, d’une part, à la variation relative (p 漣 p) /p de la pression, d’autre part, à la différence de température T 漣 T entre l’air de la bulle et l’air ambiant.

Critères de stabilité

Considérons maintenant la répartition verticale des températures de l’air telle qu’elle résulte d’un sondage de température effectué à l’aide d’un ballon emportant un thermomètre (et un baromètre, la connaissance simultanée de la pression et de la température à chaque niveau permettant, d’après l’hypothèse hydrostatique, de calculer les altitudes). La pression diminue constamment avec l’altitude; pour la température, il en va différemment selon la stratification verticale des masses d’air. Il arrive en effet que la température augmente parfois avec l’altitude (inversion de température) dans certaines couches atmosphériques, mais, cependant, en général elle décroît, tout au moins dans la couche appelée troposphère qui, sous les latitudes tempérées, s’étend du voisinage du sol jusqu’à 10 ou 12 kilomètres.

Si cette décroissance de température est supérieure à 1 ⁰C par 100 mètres de dénivellation, il est aisé de voir (fig. 5) qu’une particule d’air partant d’un niveau déterminé à la même température que l’air environnant se trouvera systématiquement plus chaude que l’air ambiant si elle monte et plus froide que l’air ambiant si elle descend. Cela est vrai pour une particule d’air non saturé et, a fortiori, pour une particule d’air saturé. Toute particule tend dans ce cas à s’éloigner de son niveau initial. Donc, si le gradient vertical de température est supérieur au gradient adiabatique sec (1 ⁰C pour 100 m), l’air est instable, que la particule en mouvement soit saturée ou non. On dit qu’il y a instabilité absolue.

Si la décroissance verticale de température est inférieure au gradient adiabatique saturé (correspondant à la pression et à la température considérées), on voit de même (fig. 6) qu’une particule saturée (et a fortiori une particule non saturée) est toujours plus froide que l’air ambiant si elle est déplacée vers le haut et plus chaude que l’air ambiant si elle est déplacée vers le bas. Dans les deux cas elle tend à rejoindre son niveau initial. Donc, si le gradient vertical de température est inférieur au gradient adiabatique saturé, l’air est stable, que la particule en mouvement soit saturée ou non. On dit qu’il y a stabilité absolue.

Dans le cas intermédiaire, entre l’instabilité absolue et la stabilité absolue, il y a instabilité conditionnelle: l’air est stable vis-à-vis d’une particule d’air non saturé et instable vis-à-vis d’une particule d’air saturé.

Instabilité conditionnelle ou sélective

Le cas de l’instabilité conditionnelle est le plus intéressant parce qu’il est le plus fréquent dans l’atmosphère. En effet, la décroissance moyenne normale de la température de la troposphère est d’environ 0,65 ⁰C pour 100 mètres. C’est d’ailleurs cette valeur qui est utilisée pour définir l’atmosphère standard qui est prise en considération pour graduer les altimètres d’avions.

Les cas de couches atmosphériques absolument instables sont rares et de courte durée; les gradients suradiabatiques (supérieurs à 1 ⁰C pour 100 m) s’observent le plus souvent au voisinage du sol en été. En revanche, on rencontre plus fréquemment des couches d’air absolument stables; c’est le cas en particulier des inversions de températures (la température croît avec l’altitude) et des zones de subsidence anticycloniques (c’est la raison pour laquelle le ciel est fréquemment clair dans les anticyclones). Pour étudier de façon plus détaillée l’instabilité conditionnelle, il est commode de prendre en considération le travail mis en jeu lors du déplacement vertical d’une particule d’air.

Figurons sur un émagramme (fig. 7) la répartition verticale A B D de la température déduite d’un sondage effectué dans une certaine masse d’air. Dans le cas de l’instabilité conditionnelle, la courbe A B D, donnant la répartition verticale réelle de la température, a une pente comprise entre celle de l’adiabatique sèche et celle de l’adiabatique saturée. Supposons que la particule située en A, supposée non saturée, subisse une impulsion verticale dirigée vers le haut. Son point figuratif se déplace de A vers C et l’on voit qu’elle est toujours plus froide que l’air environnant; elle dépense donc de l’énergie puisque la force F qui la sollicite est dirigée vers le bas, en sens inverse du déplacement.

Si son énergie initiale est suffisante, elle atteindra son point de condensation supposé en C et, à partir de ce moment-là, son point figuratif suivra l’adiabatique saturée C D F qui passe en C. Cette adiabatique saturée coupe la courbe du sondage A B D en D. On voit qu’au-dessus de D la température de la particule ascendante devient supérieure à celle de l’air ambiant et la particule continue à s’élever spontanément en acquérant même de l’énergie.

En résumé, alors que la particule ascendante a constamment dépensé de l’énergie pour monter jusqu’en D, et a par conséquent constamment été freinée, elle acquiert de l’énergie au-dessus de D et se trouve accélérée. Elle s’élèvera ainsi jusqu’au niveau où elle rencontrera une couche stable qui l’arrêtera. Rappelons que l’échelle des pressions sur un émagramme est une échelle relative (logarithmique), de sorte que le travail:

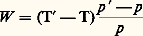mis en jeu lors de l’ascension de la particule de A en D se trouve être exactement mesuré par la surface du triangle curviligne A C D. C’est là un des nombreux avantages de l’émagramme.

En conclusion, toute particule issue de A et dotée d’une énergie initiale suffisante pour atteindre le niveau D se comportera comme une particule instable. En revanche, toute particule non dotée d’une énergie suffisante dépensera cette énergie avant d’atteindre D et s’arrêtera à un niveau intermédiaire entre A et D. Plus froide que l’air environnant, elle sera alors rappelée vers A et se comportera donc comme une particule stable.

Nuages convectifs et théorie de l’entraînement

La théorie de l’instabilité qui vient d’être esquissée permet l’étude de la formation des nuages (cumulus et cumulo-nimbus) dus à la convection thermique. Elle permet de prévoir l’altitude de leur base et de leur sommet, l’heure de leur apparition, leur évolution au cours de la journée; elle permet aussi de calculer la température à chaque niveau dans le nuage ainsi que la quantité d’eau condensée dans le nuage et la probabilité que ces nuages donnent lieu à des averses. En fait, les différences entre les valeurs calculées et observées de ces paramètres ont conduit à imaginer que, lors de leur mouvement, les particules ascendantes (bulles) se mélangent plus ou moins sur leur bordure avec de l’air ambiant. C’est la théorie de l’entraînement; elle conduit à ce résultat: la décroissance de température dans un cumulus ne s’effectue pas selon la loi de l’adiabatique saturée comme l’indiquerait la théorie simplifiée précédente, mais selon une loi intermédiaire entre la loi adiabatique sèche et la loi adiabatique saturée. De plus, par suite du mélange avec l’air environnant, la teneur en eau condensée du nuage est moindre et les sommets prévus du nuage sont moins élevés. Ces résultats généraux sont plus proches de la réalité, mais la difficulté pratique est de fixer le taux d’entraînement de l’air ambiant qui, en tout état de cause, doit être variable et dépendra de la grosseur des bulles ascendantes.

Encyclopédie Universelle. 2012.